Champ électrique

Mouvement dans un champ uniforme - Physique-Chimie Spécialité

Exercice 1 : Calculer le travail d'une force, électron dans un condensateur (q, champ élec, distance)

Un proton de charge \( q = 1,60 \times 10^{-19} C \) passe entre 2 plaques d'un condensateur C qui forme un champ électrique uniforme de valeur \( 40 V\mathord{\cdot}cm^{-1} \).

La trajectoire du proton est présentée sur le schéma ci-dessous :

Déterminer le travail de la force électrique entre le point \( A \) et le point \( B \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.

Exercice 2 : Calculer des champs électriques et des forces dans un condensateur

Dans tout l'exercice, l'unité retenue pour exprimer l'intensité d'un champ électrique est le \( V \cdot m^{-1} \).

Soit un champ électrostatique \( \overrightarrow{E} \) uniforme à l'intérieur d'un condensateur.
Dans ce condensateur, une particule de charge \( q = 3\mbox{,}1\:\text{mC} \) subit une force \( \overrightarrow{F} \) telle que \( F = 8\mbox{,}0 \times 10^{-2}\:\text{N} \).

Quelle est la valeur \( E \) de l'intensité électrique du champ ?
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Calculer la valeur \( E' \) du champ électrostatique entre les armatures parallèles du condensateur distantes de \( 0\mbox{,}20\:\text{mm} \) quand le condensateur est chargé sous une tension de \( 5\mbox{,}0\:\text{V} \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
En déduire la valeur \( F' \) de la force que subirait une particule de charge \( q' = 5\mbox{,}0\:\text{nC} \) placée entre les armatures de ce condensateur.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.

Exercice 3 : Bac Spécialité 2023 (Métropole, septembre, jour 2) - Exercice 3 - Imprimante à jet d’encre continu

Imprimante à jet d’encre continu

De nombreuses applications technologiques, dans des domaines très variés, reposent sur l’utilisation d’un champ électrique.
L’objectif de cet exercice est d’étudier le principe de fonctionnement des imprimantes à jet d’encre continu dévié, principalement utilisées pour imprimer les dates d’expiration figurant sur les produits alimentaires.
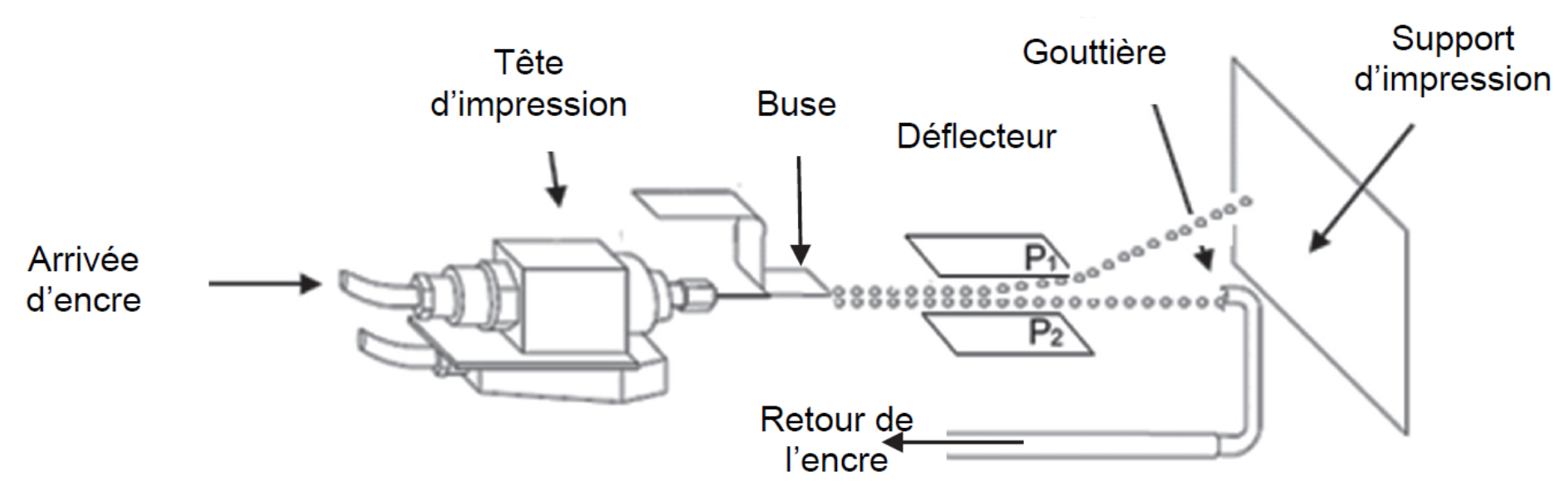
On donne sur le schéma de la figure 1, le principe de fonctionnement de l’imprimante à jet d’encre continu dévié : le jet d’encre sort de la tête d’impression par une buse qui le décompose en très petites gouttes dont certaines sont chargées électriquement.
Celles-ci passent sous un déflecteur constitué de deux plaques \(P1\) et \(P2\) parallèles, chargées électriquement, assimilables à un condensateur plan. Ces plaques dévient les gouttes chargées de leur trajectoire initiale.
Les gouttes non chargées poursuivent quant à elles leur mouvement rectiligne vers une gouttière de recyclage et sont réintégrées dans le module d’encre afin d’être réutilisées.

Schéma imprimante
Figure 1. Schéma de principe de l’imprimante à jet d’encre continu dévié (d’après le site timis.fr)

Données :

  • les mouvements sont étudiés dans le référentiel terrestre supposé galiléen associé au repère \((O, \vec{i}, \vec{k})\) représenté sur la figure 2. Les vecteurs \(\vec{i}\) et \(\vec{k}\) sont unitaires ;
  • on considère que la charge électrique et la masse des gouttes d’encre restent constantes entre la buse et le support d’impression ;
  • masse d’une goutte d’encre : \(m = 2×10^{-10}\: \text{kg} \) ;
  • charge électrique d’une goutte : \(q = -3×10^{-13}\:\text{C}\) ;
  • valeur de la vitesse d’éjection des gouttes d’encre : \(v_{0} = 20\:\text{m/s}\) ;
  • longueur des plaques du déflecteur : \(L = 3\:\text{cm}\) ;
  • distance entre le déflecteur et le support d’impression : \(D = 1\:\text{cm}\) ;
  • le champ électrique est supposé uniforme dans le déflecteur, il s’écrit \(\vec{E} = – E\vec{k}\) avec \(E = 9 \times 10^{5}\:\text{V}\mathord{\cdot}\text{m}^{-1}\) ;
  • le champ électrique est nul à l’extérieur du déflecteur ;
  • hauteur moyenne d’un caractère imprimé : \(h = 3\:\text{mm}\) ;
  • intensité de la pesanteur : \(g = 9,81\: \text{m}\cdot \text{s}^{-2}\).

On étudie le mouvement d’une goutte d’encre \(G\), supposée ponctuelle, de masse \(m\) et de charge \(q\) négative

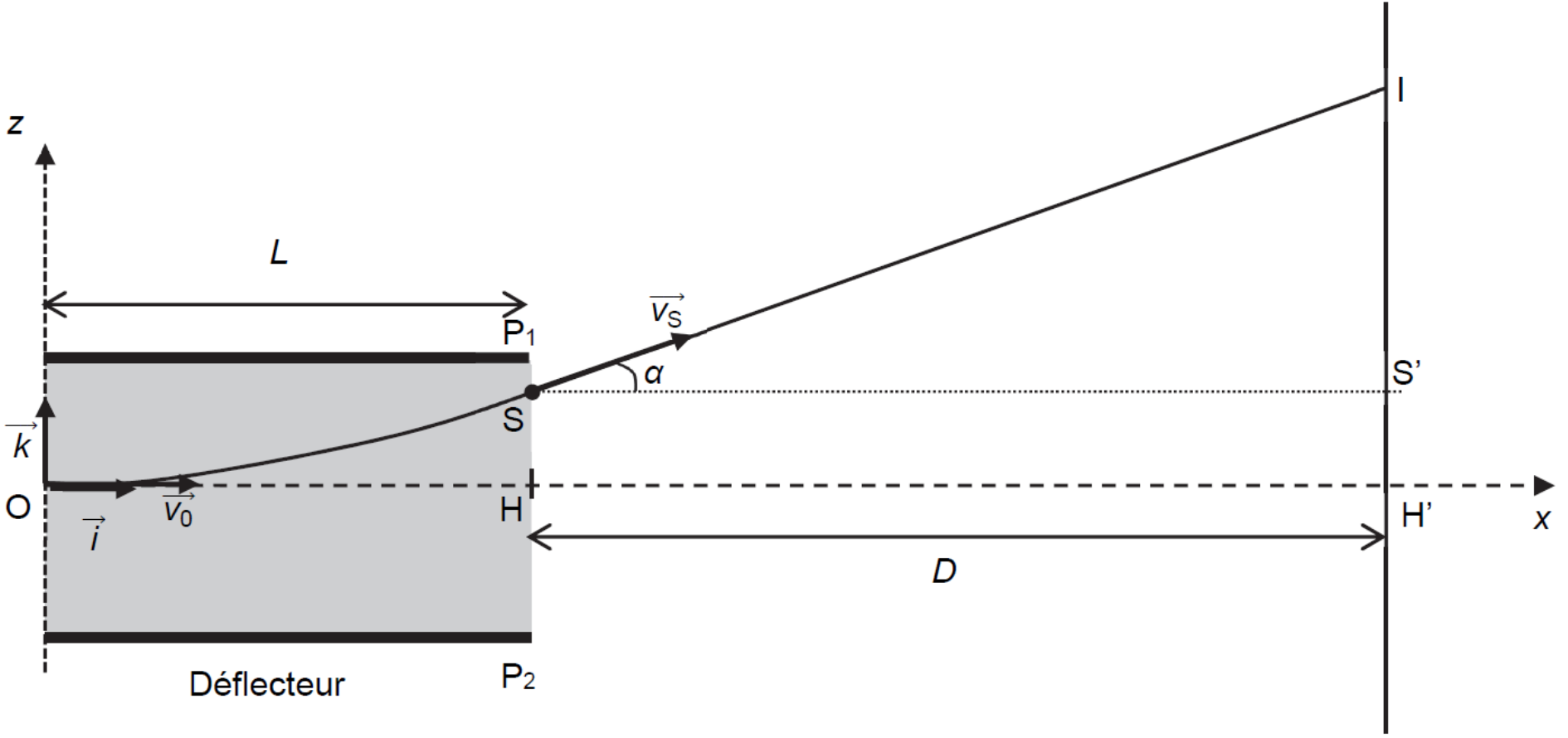
Graphique du mouvement du jet d'encre
Figure 2. Schéma de la trajectoire de la goutte \(G\)

À la date \(t_{0} = 0\:\text{s}\), la goutte d’encre \(G\) pénètre dans la zone de champ électrique uniforme au niveau du point \(O\) avec une vitesse initiale notée \(\vec{v_{0}} = v_{0} \vec{i} \).
On suppose que l’action mécanique de l’air est négligeable devant les autres actions.

1. a Indiquer les signes des charges portées par les plaques \(P1\) et \(P2\) sachant que la goutte chargée négativement est déviée vers le haut (sens des \(z\) croissants).
Le premier symbole correspondant à \(P1\) et le second à \(P2\).
1. b En déduire l’orientation du vecteur champ électrique \(\vec{E}\).

On suppose que la valeur du poids de la goutte d’encre \(G\) est négligeable par rapport à celle de la force électrique subie dans le déflecteur.
Établir l’expression du vecteur accélération \(\vec{a_{G}}\) de la goutte d’encre en fonction de la masse \(m\), de la charge \(q\) et du vecteur champ électrique \(\vec{E}\) entre les plaques du déflecteur.

2. a \(a_{Gx}(t)\) est égale à :
On donnera directement l’expression.
2. b \(a_{Gz}(t)\) est égale à :
On donnera directement l’expression.

Donner les expressions des équations horaires \(x_{G}(t)\) et \(z_{G}(t)\) du mouvement de la position de la goutte d’encre \(G\) dans le déflecteur.

3. a \(x_{G}(t)\) est égale à :
On donnera directement l’expression.
3. b \(z_{G}(t)\) est égale à
On donnera directement l’expression.
4. a Exprimer en fonction de \(L\) et \(v_{0}\) la date \(t_{S}\) à laquelle la goutte d’encre \(G\) sort du déflecteur.
On donnera directement l’expression.
4. b Calculer la valeur numérique de \(t_{S}\).
On donnera le résultat en s avec le nombre de chiffres significatifs permis par les données de l'énoncé.
4. c Calculer la valeur de la déviation \(HS\).
On donnera le résultat en mm avec le nombre de chiffres significatifs permis par les données de l'énoncé.

Donner les coordonnées du vecteur vitesse \(\vec{v_{S}}\) de la goutte d’encre \(G\) à la date \(t_{S}\).

5. a \(v_{x}(t_{s})\) est égale à :
On donnera le résultat en \(\text{m}/\text{s}\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.
5. b \(v_{z}(t_{s})\) est égale à :
On donnera le résultat en \(\text{m}/\text{s}\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.

On considère l’angle \(\alpha\) entre l’axe \((O_{x})\) et le vecteur vitesse \(\vec{v_{S}}\).

6 Déterminer l’expression de \(tan \alpha\) en fonction de \(q\), \(E\), \(L\), \(m\) et \(v_{0}\).
On donnera directement l’expression.

On suppose que le mouvement de la goutte entre le point \(S\) et le support d’impression est rectiligne uniforme.

7 En déduire la valeur de la hauteur \(H’I\) du point d’impact \(I\) de la goutte sur le support d’impression.
On donnera le résultat en \(mm\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.
8. a Avec les données choisies, a-t-on imprimé un caractère de hauteur plus ou moins grande que la hauteur moyenne d’un caractère imprimé ?
8. b Cocher parmi les paramètres suivants celui ou ceux qui permettent d’augmenter la taille du caractère si on les augmente.

Exercice 4 : Calculer le travail d'une force, électron dans un condensateur (q, champ élec, distance)

Un proton de charge \( q = 1,60 \times 10^{-19} C \) passe entre 2 plaques d'un condensateur C qui forme un champ électrique uniforme de valeur \( 60 V\mathord{\cdot}cm^{-1} \).

La trajectoire du proton est présentée sur le schéma ci-dessous :

Déterminer le travail de la force électrique entre le point \( A \) et le point \( B \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.

Exercice 5 : Calculer des champs électriques et des forces dans un condensateur

Dans tout l'exercice, l'unité retenue pour exprimer l'intensité d'un champ électrique est le \( V \cdot m^{-1} \).

Soit un champ électrostatique \( \overrightarrow{E} \) uniforme à l'intérieur d'un condensateur.
Dans ce condensateur, une particule de charge \( q = 9\mbox{,}0\:\text{mC} \) subit une force \( \overrightarrow{F} \) telle que \( F = 1\mbox{,}5 \times 10^{-2}\:\text{N} \).

Quelle est la valeur \( E \) de l'intensité électrique du champ ?
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Calculer la valeur \( E' \) du champ électrostatique entre les armatures parallèles du condensateur distantes de \( 0\mbox{,}80\:\text{mm} \) quand le condensateur est chargé sous une tension de \( 9\mbox{,}0\:\text{V} \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
En déduire la valeur \( F' \) de la force que subirait une particule de charge \( q' = 3\mbox{,}5\:\text{nC} \) placée entre les armatures de ce condensateur.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Revenir au choix du niveau
Kwyk vous donne accès à plus de 1 000 exercices auto-corrigés en Physique-Chimie.
Nos exercices sont conformes aux programmes de l'Éducation Nationale de la 3e à la Terminale. Kwyk permet aux élèves d'aborder les notions les plus importantes en Physique-Chimie comme l'étude des ondes et de l'optique, l'organisation et la transformation de la matière, la conservation et les transferts d'énergie et les lois de l'électricité. Les élèves peuvent travailler sur l'étude du mouvement avec des exercices de mécanique et de cinétique. Kwyk propose également de nombreux exercices d'entraînement sur les conversions et la manipulation des unités, l'écriture scientifique et l'utilisation des chiffres significatifs.

Nos exercices sont proposés sous forme de réponse libre et/ou de QCM. Afin d'assurer un entraînement efficace et pertinent aux élèves, chaque exercice est généré avec des valeurs aléatoires. Tous les ans, de nouvelles annales du brevet des collèges et du baccalauréat sont mises en ligne sur www.kwyk.fr. Les élèves peuvent s'entraîner grâce aux devoirs donnés sur Kwyk par leurs professeurs et aux devoirs générés par notre outil utilisant l'IA mais aussi grâce aux différents modules de travail en autonomie mis à disposition sur leur espace personnel.

Avec Kwyk, vous mettez toutes les chances de succès du côté des élèves.
Exercices de Physique-Chimie : préparer les examens
Brevet des collèges | Baccalauréat
S'entraîner dans d'autres matières
Mathématiques | Français
False