Exercice type Bac de Physique-Chimie
Au bonheur des hippocampes
La conservation d’hippocampes en aquarium est généralement très difficile et réservée aux
aquariophiles expérimentés. En effet, ces espèces sont souvent très fragiles, ont un régime
alimentaire complexe et sont très sensibles aux variations de températures. Par exemple,
l’hippocampe pygmée de Denise, originaire des eaux tropicales de l’océan Pacifique, vit
dans des eaux salées dont la température doit rester comprise entre \( 24 \) et \( 28 \: \text{°C} \).
Dans cet exercice, on s’intéresse à la régulation de la température d’un aquarium dont on
voudrait qu’il puisse accueillir des hippocampes pygmées.
L’aquarium étudié est décrit dans le document 1 ci-dessous. Il est fermé par un couvercle.
Ses parois latérales et son couvercle sont en plexiglass, un matériau plastique. Il est placé
dans une pièce dont l’air ambiant est à une température constante de \( 19 \: \text{°C} \). Cette
température est sensiblement plus basse que celle de \( 26 \: \text{°C} \) souhaitée pour l’eau de
l’aquarium.
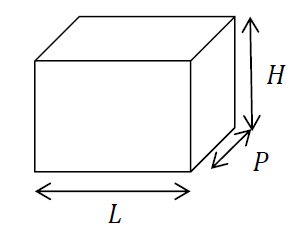
Document 1 - Description de l'aquarium
- Hauteur : \( H = 0\mbox{,}50\:\text{m} \)
- Longueur : \( L = 0\mbox{,}60\:\text{m}\)
- Profondeur : \( P = 0\mbox{,}50\:\text{m}\)
-
Parois en plexiglass (PMMA) :
- Épaisseur : \( 𝑒_{paroi} = 8,0 \: \text{mm} = 8,0 × 10^{−3} \: \text{m} \)
- Conductivité : \( 𝜆_{PMMA} = 0,17 \: \text{W} ⋅ \text{m}^{−1} ⋅ \text{°C}^{−1} \) - Température souhaitée pour l’eau de l’aquarium : \( 𝜃_{eau} = 26 \: \text{°C} \)
- Température de l’air ambiant : \( 𝜃_{air} = 19 \: \text{°C} \) (supposée constante)
Afin de stabiliser la température de l’eau, un système de chauffage électrique est introduit.
Il est combiné à un dispositif de circulation d’eau pour avoir une température de l’eau
uniforme dans l’aquarium.
Dans un premier temps, on souhaite déterminer la puissance que doit fournir ce système
de chauffage électrique pour maintenir la température de l’eau. Pour cela, il est nécessaire
d’estimer les pertes thermiques que le système de chauffage doit permettre de compenser.
On considère que les pertes thermiques se font principalement au travers des parois de
l’aquarium.
On donnera le nom de chacun des modes de transfert séparés par un point-virgule sans majuscule.
On donnera le résultat suivi de l'unité qui convient.
Dans la suite de l’exercice, on étudie plus particulièrement la contribution de la conduction
thermique au travers des parois et du couvercle de l’aquarium.
À cet effet, on rappelle quelques lois dont on admet qu’elles sont valides dans la situation
étudiée :
- Puissance thermique de conduction Φ (exprimée en watt) au travers d’une paroi de
résistance \( 𝑅_{th} \) soumise à une différence de température \( Δ𝜃 \) :
\[ Φ = \frac{Δ𝜃}{𝑅_{th}} \]
- Résistance thermique \( 𝑅_{th} \) d’un ensemble de parois d’épaisseur \( 𝑒 \), et de surface totale
\( 𝑆_𝑇 \), réalisée dans un même matériau de conductivité thermique \( 𝜆 \) :
\[ 𝑅_{th} = \frac{𝑒}{𝑆_𝑇 ⋅ 𝜆} \]
Par ailleurs, on considère que la conduction thermique se fait exclusivement par les parois
latérales et le couvercle (la surface en contact avec la table ne contribue pas).
On donnera le résultat suivi de l'unité qui convient.
On donnera le résultat suivi de l'unité qui convient.
On donnera le résultat suivi de l'unité qui convient.
Pendant la journée, en particulier en période estivale, on envisage de chauffer l’aquarium
avec le rayonnement du Soleil en plaçant l’aquarium devant une fenêtre bien exposée. Cela
permettrait de ne pas utiliser le système de chauffage électrique.
Dans les conditions décrites, par une belle journée d’été, on peut estimer la puissance
thermique d’origine solaire absorbée par l’eau de l’aquarium à environ \( 𝑃_S = 30 \: \text{W} \).
Afin de préciser l’évolution de la température au cours de la journée, on réalise une étude
dynamique. Grâce au dispositif de circulation d’eau, on suppose que la température de l’eau
dans l’aquarium est la même partout. On note \( 𝜃(𝑡) \) cette température.
À l’instant \( 𝑡 = 0 \) :
L’eau de l’aquarium est à la température \( 𝜃_0 \) : \( 𝜃(𝑡 = 0) = 𝜃_0 = 26 \: \text{°C} \).
On place l’aquarium au Soleil. Il reçoit la puissance de rayonnement \( 𝑃_S = 30 \: \text{W} \).
On coupe le système de chauffage électrique.
Par ailleurs, on suppose que la pièce dans laquelle se trouve l’aquarium est bien isolée et
régulée en température, ce qui permet de supposer que la température de l’air ambiant est
constante et égale à \( 𝜃_{air} = 19 \: \text{°C} \).
On note \( 𝑚 \) la masse d’eau de mer dans l’aquarium et \( 𝑐 \) la capacité thermique de cette eau.
En utilisant le premier principe de la thermodynamique appliqué à l’eau de l’aquarium, on
établit l’équation dynamique du système :
\[ 𝑚 ⋅ 𝑐 ⋅\frac{d𝜃(𝑡)}{d𝑡} + \frac{𝜃(𝑡)}{𝑅_{th}} = \frac{𝜃_{air}}{𝑅_{th}} + 𝑃_𝑆 \]
En tenant compte de la condition initiale, la solution de cette équation s’écrit :
\( 𝜃(𝑡) = 𝜃_0 𝑒^{−\frac{𝑡}{𝜏}} + (𝜃_{air} + 𝑅_{th} ⋅ 𝑃_𝑆) (1 − 𝑒^{−\frac{𝑡}{𝜏}}) \) avec \( 𝜏 = 𝑚 ⋅ 𝑐 ⋅ 𝑅_{th} \)
- \( 𝑚 = 100 \: \text{kg} \)
- \( 𝑐 = 3 930 \: \text{J} ⋅ \text{kg}^{−1} ⋅ \text{°C}^{−1} \)
- \( 𝜃_{air} = 19 \: \text{°C} \)
- \( 𝑃_𝑆 = 30 \: \text{W} \)
- \( 𝑅_{th} =3\mbox{,}4 \times 10^{-2}\:\text{°C}\mathord{\cdot}\text{W}^{-1} \)
On donnera le résultat suivi de l'unité qui convient.
On donnera le résultat suivi de l'unité qui convient.
On rappelle que la température initiale de l’aquarium est \( 𝜃_0 = 26 \: \text{°C} \).
On donnera le résultat suivi de l'unité qui convient.
Exemple de réponse : \( 6 \text{h} 52 \: \text{min} \).


